por Marco Goulart

Apresentação

Nosso objetivo com este artigo é apresentar uma revisão estendida sobre o Modelo de Desconto de Dividendos. É um texto técnico para o estudante de finanças. O texto foi desenvolvido de forma didática, avançando dos conteúdos mais simples para os mais complexos. Consideramos que com conhecimentos básicos de matemática é possível compreender o texto como um todo. O conhecimento sobre demonstrativos financeiros e indicadores econômico-financeiros pode auxiliar no entendimento mais aprofundado do assunto.

Importância: um bom modelo para começar

Este tipo de modelo é importante pois permite encontrar um valor justo (ou intrínseco) para um ativo financeiro, como ações de uma empresa. A partir do resultado deste modelo pode-se comparar o valor justo com as ofertas encontradas no mercado, ou o preço de negociação das ações (no caso de uma empresa com capital aberto). Se o valor justo é superior ao preço encontrado, então teríamos uma boa oportunidade de aquisição. Se o valor justo é inferior ao preço encontrado, então seria uma boa alternativa vender a empresa, ou ficar de fora do mercado.

O Modelo de Desconto de Dividendos (MDD) foi o primeiro modelo de precificação de ativos baseado no conceito de valor presente de fluxos financeiros. É um modelo simples e por isso útil para aqueles que querem iniciar os estudos sobre técnicas de precificação de ativos.

A partir do entendimento deste modelo é mais fácil avançar para o estudo de outros modelos, que envolvem maior complexidade, como o do fluxo de caixa descontado da empresa e do acionista.

Iniciar o aprendizado de avaliação de ativos por este modelo também ajuda a entender as influências que as estimativas de taxas de desconto e crescimento exercem sobre o valor final encontrado nas avaliações.

Um fluxo financeiro descontado: o que é?

Este conceito parte do pressuposto de que o dinheiro tem valor no tempo, por exemplo, $100 daqui a um ano devem valer menos do que $100 hoje. A forma de “descontar” este valor no tempo é a aplicação do “preço do dinheiro”, ou juros. Supondo no nosso exemplo que o juro é de 10% ao ano, então o valor de $100 daqui a um ano, hoje, é igual a $90,91. Estes juros são compostos, ou seja, incorrem de forma exponencial (juros sobre juros).

A equação matemática para descontar um valor que está no futuro para o valor no presente é:

No caso de um fluxo financeiro teríamos a soma de todos os valores que ocorrem no futuro descontados para o presente, assim a equação ficaria da seguinte forma:

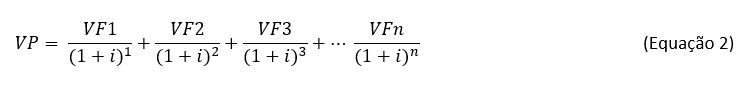
Vamos ver mais a frente que o MDD nada mais é do que uma aplicação desta equação, supondo um fluxo constante e infinito.

Breve histórico: Gordon levou a fama

O conceito de valor presente de um fluxo financeiro foi desenvolvido por diversos autores ao longo das primeiras décadas de 1900. Talvez os autores mais conhecidos que de alguma forma abordaram o assunto são: Irvin Fisher (1930), John Maynard Keynes (1936), e John Burr Williams (1938). Mas o uso dos dividendos em crescimento como “o parâmetro” do fluxo financeiro de um ativo foi desenvolvido por David Durand (1957) e Myron Gordon (1962). Este último escreveu um livro sobre o assunto dando o seu nome ao modelo: Modelo de crescimento de Gordon. Por isso hoje o MDD também é chamado de modelo de Gordon.

Diferente das Equações 1 e 2, no modelo de Gordon a taxa de desconto é composta por duas variáveis: a taxa de retorno exigida pelo investidor, e a taxa de crescimento esperada para os dividendos distribuídos pela empresa.

O MDD: parâmetros principais

De acordo com o MDD o cálculo do valor de uma empresa pode ser baseado no fluxo financeiro que é distribuído aos seus acionistas. Os dividendos são a parcela do lucro da empresa que pertence aos acionistas, e, portanto, são considerados como o fluxo.

A versão com crescimento do MDD considera que esses dividendos são constantes e crescem indefinidamente. Esta suposição de que o dividendo continuará sendo pago indefinidamente parte da lógica de que é do propósito de uma empresa a continuidade de suas atividades. Como a economia cresce de forma contínua, os dividendos também o fazem: é a taxa de crescimento.

Como vimos, esses fluxos (dividendos) devem ser descontados a uma determinada taxa. A taxa considerada no MDD é o custo de capital próprio, que é a taxa para a qual os acionistas estão dispostos a dispor seus recursos para a empresa. Em geral essa taxa é representada pela taxa básica de juros de uma econômica (taxa livre de risco) adicionada de um prêmio pelo risco que o acionista corre ao destinar seus recursos para a empresa.

Assim temos o MDD baseado nos três parâmetros: dividendos (fluxo), e custo de capital próprio menos crescimento, que compõem a taxa de desconto:

O MDD é “sem crescimento” ou com “crescimento zero” quando não é aplicada uma taxa “g”, neste caso a Equação 1 é o próprio MDD.

Uma perpetuidade

O leitor deve ter percebido que na Equação 3 não temos diversos fluxos, como na Equação 2. Isso ocorre porque o MDD parte do pressuposto de continuidade, onde fluxo é infinito. Esta característica de um fluxo também é chamada de perpetuidade. Se realizássemos o cálculo para milhares de fluxos perceberíamos que quanto mais distante no tempo, menor é o valor presente do fluxo, e que o resultado das duas equações seria igual.

Continuando no nosso exemplo de aplicação da Equação 1, vamos trazer novamente os $100 para o valor presente. Mas agora vamos considerar que esse valor está no período 90, ou seja, que receberíamos o valor daqui a 90 anos: Qual é o valor de receber $100 daqui a 90 anos, hoje?

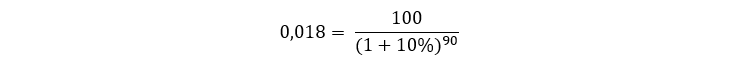
Receber $100 daqui a 90 anos tem um valor hoje de somente $0,018.

Nesta planilha apresento a comparação entre as duas equações, mostrando que os valores são iguais quando há a suposição de continuidade indefinida dos fluxos.

Exemplo de aplicação do MDD

Com base nos últimos resultados da empresa PGB S.A. você estimou que haverá uma distribuição de dividendos no próximo ano de $ 5 por ação, e que estes dividendos vão crescer de forma constante no mesmo ritmo da economia do país, medida pelo PIB. Sua expectativa de crescimento do PIB, incluindo a inflação, para os próximos anos é de 6% ao ano. Existem alternativas de investimento de baixo risco disponíveis na economia que remuneram a uma taxa de 10% ao ano. Considerando o risco de investir na PGB S.A., a taxa de retorno estipulada por você é de 15% ao ano. Qual seria o valor justo da PGB S.A.?

Utilizando a Equação 3 temos:

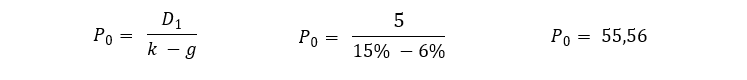
O preço justo da ação da PGB S.A. é de $ 55,56. Mas e se as taxas de crescimento e desconto (custo do capital próprio) fossem diferentes, o mesmo ocorrendo com o dividendo? Como isso alteraria o valor da ação da PGB S.A.?

Análise de sensibilidade do MDD

Essa análise é interessante pois mostra como o modelo é sensível a alterações nestas taxas. Na tabela abaixo apresentamos os valores encontrados para diversos cenários (planilha aqui).

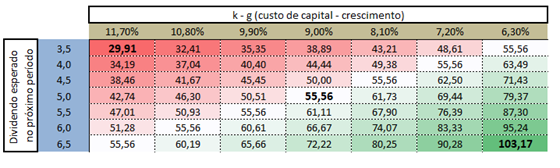
Propositalmente estamos variando tanto os dividendos quanto a taxa de desconto em 10%, 20 e 30%. Em cada célula da tabela temos um cenário diferente, mas podemos perceber que em função da forma como alteramos as variáveis temos diversos cenários equivalentes. Por exemplo, se a taxa de desconto ficar em 8,1%, mas a empresa pagar somente $4,5 em dividendos, ainda assim o preço da ação seria $55,56.

Também é interessante notar que o modelo é bastante sensível: considerando os dividendos estáveis em $5, quando diminuímos a taxa em 10%, de 9% para 8,1%, o preço subiu 11% ($61,73). Quando diminuímos a taxa em 30%, de 9% para 6,3%, o preço subiu 49% ($79,93).

Naturalmente, considerando a Equação 3, há uma relação direta dos dividendos e da taxa de crescimento com o preço, e inversa do custo de capital com o preço. Ou seja, quanto maior o dividendo e a taxa de crescimento maior será o preço, e quanto menor o custo de capital maior será o preço.

Como uma empresa continua crescendo?

No nosso exemplo da PGB S.A. apresentamos “g” como variável já conhecida. Mas podemos aprofundar o entendimento da origem desta variável no modelo. Para isso é útil o conhecimento básico sobre demonstrativos financeiros e indicadores de desempenho econômico-financeiros. Não vamos explorar estes assuntos aqui, então partimos do pressuposto de que o leitor domina estes assuntos.

Vimos que os dividendos são uma parcela dos lucros que são distribuídos aos acionistas. A outra parcela, que não é distribuída, fica na empresa e é utilizada para reinvestimento. Sabemos que o reinvestimento dos lucros é a principal fonte de recursos de uma empresa no longo prazo. Uma parte do lucro reinvestido deve simplesmente repor os ativos que depreciam (ex: desgaste de uma máquina), e o excedente pode ser aplicado na aquisição de novos ativos que geram novas receitas (ex: novas máquinas). Este excedente pode ser calculado através da taxa de retenção. Para calcular a taxa de retenção basta subtrair de 100% a proporção de lucros que a empresa distribui aos seus acionistas, chamado payout.

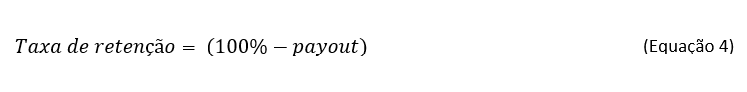
Esta fórmula é uma simplificação, mesmo se a taxa de retenção calculada pela Equação 4 for de 90%, se todo o recurso retido for necessário para a manutenção da atividade da empresa, então não é coerente esperar que os lucros cresçam no futuro.

Outro ponto importante para o cálculo do crescimento dos lucros é a taxa de retorno do valor que fica retido e é reaplicado na empresa. O retorno sobre o patrimônio líquido (ROE – Return on Equity) pode ser utilizado para encontrar este valor.

O que esta relação mostra é que quanto menor o lucro da empresa em relação ao capital investido pelo acionista (patrimônio líquido), menor será o potencial de distribuição de dividendos no futuro.

Finalmente chegamos na Equação 6, que mostra a relação entre a retenção de lucros e a taxa de retorno dos valores reinvestidos para o crescimento da empresa.

No nosso exemplo da PGB S.A. consideramos que a empresa iria crescer no mesmo ritmo da economia medido pelo PIB, 6% ao ano. Mas seria esse valor seria condizente com a realidade da empresa? Não seria coerente supor que uma empresa cresce indefinidamente mais do que a economia, pois neste caso em algum momento ela se tornaria maior do que a economia do país. Mas a PGB S.A. poderia ter um crescimento inferior ao da economia, então o cálculo de “g” poderia nos ajudar a entender o que acontece com a empresa.

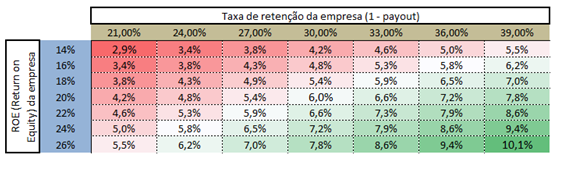
Observe na tabela de análise de sensibilidade que se a PGB S.A. tiver um ROE inferior a 20% e uma taxa de retenção inferior a 30% ela não irá crescer no mesmo ritmo estimado da economia do país (6% ao ano). Quanto menor o ROE, maior será a parcela do lucro que a empresa deve reinvestir para obter crescimento, e consequentemente menor será o dividendo distribuído ao acionista.

No MDD a suposição é que todos estes valores de taxa de retenção e ROE são constantes para a empresa, de forma que sua aplicação é recomendada somente para empresas em condição de estabilidade.

Quanto maior o crescimento, menor o dividendo hoje

Esta afirmação intuitiva é pertinente para o MDD pois quanto maior o crescimento da empresa, mais tempo o investidor irá levar para recuperar o capital investido. O crescimento maior é melhor se considerarmos o preço mais elevado para a ação, mas pior se considerarmos o risco de o investidor não receber: quanto mais no futuro o fluxo de dividendo, mais imprevisível é o seu recebimento.

Vamos supor que além da PGB S.A. existe a alternativa de investir em ações da SMB S.A. A SMB possui as mesmas características da PGB, exceto pelo crescimento dos dividendos que é de 9,5%. Assim teríamos os seguintes preços para a ação da PGB S.A. e da SMB S.A.

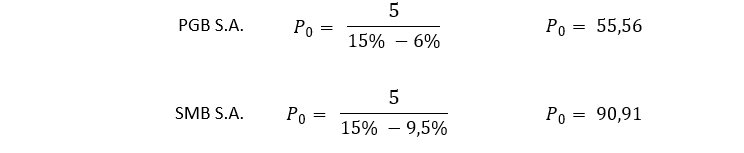
Caso as ações das duas empresas fossem oferecidas pelo valor justo calculado pelo MDD, a recuperação do capital do investidor ocorreria antes no caso da PGB S.A., já que seu retorno em dividendos é superior. Este retorno nada mais é do que o valor recebido em dividendos em relação ao preço pago na ação (5 dividido por 55,56 no caso da PGB S.A.).

Nesta planilha apresento a análise desta situação na forma gráfica.

Esta situação apresenta uma das limitações do MDD. Encerramos aqui este artigo e em um próximo artigo vamos explorar um caso real, abordando outros pontos que merecem destaque no uso do modelo de desconto de dividendos.